
La matematica? È molto difficile dare una definizione di Matematica. Una definizione che mi piace: la Matematica è la disciplina per antonomasia, almeno quella in cui la ragione ha una posizione predominante.
Per me: la matematica è una sfida con te stesso, con la tua capacità di analisi, con la tua intuizione, e tu devi essere in grado di arrivare esattamente nel cuore del “problema”, non basta arrivargli vicino, devi coglierlo esattamente al centro: la matematica non ti consente il minimo errore.
È una sfida affascinante ed emozionante, poiché ti propone ostacoli via via sempre più difficili da superare e quando li hai superati provi grande soddisfazione.
Sfida ed emozione del risultato: la matematica è, prima di tutto, questo, per me.
E se è una sfida, bisogna fare di tutto per vincerla. La matematica è anche una grande prova di “rigore”, devi disciplinare le tue azioni mentali, devi indirizzarle verso un percorso ben preciso, senza lasciare alcunché al caso. Per questo nel gergo comune si parla di “rigore matematico”.
Tutto ciò non è facile, richiede fatica, concentrazione, sacrificio.
La matematica è esclusiva, quando sei con lei devi pensare solo a lei, non puoi concederti alcuna distrazione.
Per tutte queste cose, al di là delle oggettive difficoltà, la matematica è spesso odiata, perché è dura, a volte addirittura spietata. Alla fine però sa essere generosa, perché ti dispensa soddisfazione, appagamento, orgoglio per essere arrivato al risultato inseguito.
A me piace molto, forse perché anch’io so disciplinare le mie azioni, so essere rigoroso, ho la forza di sacrificarmi, se necessario, sono orgoglioso.
La Matematica può essere anche un gioco, un bellissimo passatempo, ma richiede sempre e comunque concentrazione, fatica.
La Matematica è la vita, perché la vita è tutto ciò che è la Matematica: sfida, emozione, disciplina, rigore, esclusività, fatica, sacrificio, spietatezza, generosità, soddisfazione, appagamento, gioco (poche volte, purtroppo).
ALCUNI ESEMPI DELLA MATEMATICA CHE PIACE A ME
Spesso un “problema” può essere risolto seguendo un percorso più semplice o uno più difficile, dipende solo dalla tua abilità.
Sia da risolvere la seguente potenza di binomio:
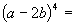
Potrei svolgerla come prodotto di due potenze aventi per esponente 2
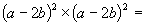 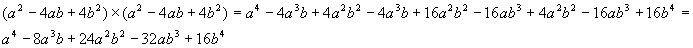
oppure, più difficile ma più bello, considerando che il polinomio risultato deve essere ordinato secondo le potenze decrescenti del primo termine e quelle crescenti del secondo e i coefficienti dei vari termini devono essere, in base al triangolo di Tartaglia, 1,4,6,4,1 ed allora il polinomio può essere così scritto:
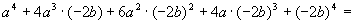
i segni che, già in partenza, so essere alternati, vengono di conseguenza
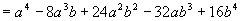
-----------------------------------------------------------------------------------------------------------------------
Sia da risolvere la seguente disequazione: 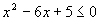
Potremmo dire subito quali sono i valori che la soddisfano, dopo aver calcolato le radici della equazione relativa.
Li vogliamo invece individuare rappresentando sul piano cartesiano la funzione 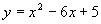 che sappiamo essere una parabola. che sappiamo essere una parabola.
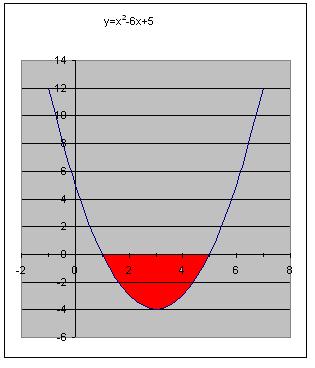
nel grafico dobbiamo verificare per quali valori di x la funzione assume valori minori o uguali a 0, cioè valori negativi:
sono quelli indicati in rosso e quindi la disequazione è soddisfatta per 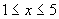 come era facilmente verificabile subito. come era facilmente verificabile subito.
----------------------------------------------------------------------------------------------------------------------
Sia da risolvere il seguente sistema:
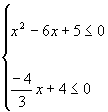

 
Vogliamo individuare i valori di x che soddisfano le due disequazioni, non attraverso la normale discussione che si fa dopo aver individuato le radici delle relative equazioni, ma rappresentando sul piano cartesiano le due funzioni che sappiamo essere quella di una parabola e di una retta
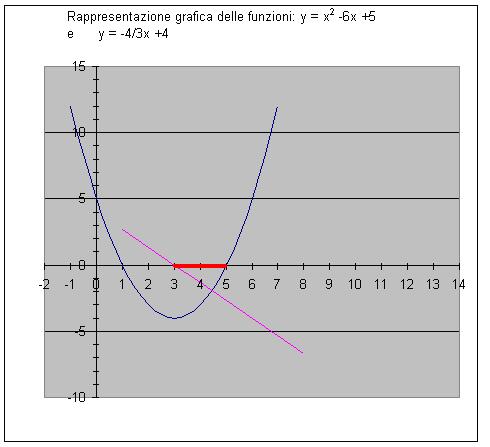
Come abbiamo visto, la prima disequazione è soddisfatta per 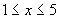 mentre la seconda per mentre la seconda per 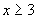 ; considerando allora le due funzioni nei loro valori negativi, come si può vedere dal grafico i valori di x che le soddisfano contemporaneamente sono compresi tra 3 e 5 e quindi il sistema è soddisfatto da ; considerando allora le due funzioni nei loro valori negativi, come si può vedere dal grafico i valori di x che le soddisfano contemporaneamente sono compresi tra 3 e 5 e quindi il sistema è soddisfatto da 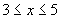 (tratto in rosso) (tratto in rosso)
A questo punto vogliamo calcolare l’equazione della retta tangente alla parabola nel punto P(2;-3)
La generica retta passante per tale punto avrà la seguente equazione: y+3 = m(x-2) e quindi dobbiamo risolvere il seguente sistema:
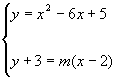
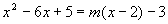
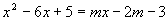
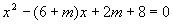
tale equazione dovrà avere necessariamente due radici coincidenti x1 = +2 e x2 = +2 poiché il punto d’incontro è noto ed ha ascissa +2
possiamo allora scrivere
x1 + x2 = 4
x1 · x2 = 4
ricordando che in una equazione di secondo grado a discriminante non negativo si ha
x1 + x2 = -b/a e x1 · x2 =c/a possiamo scrivere:
6 + m = 4
2m + 8 = 4
entrambe le equazioni hanno come soluzione m = -2
quindi l’equazione della tangente è: y = -2x +1
la rappresentazione grafica è la seguente:
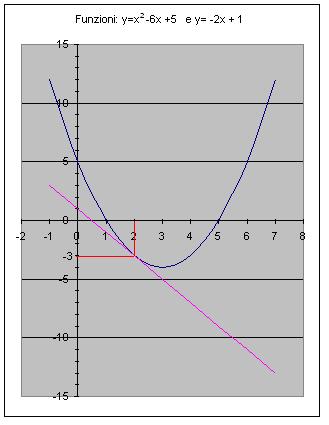
l’equazione della tangente può essere trovata anche in un’altra maniera: calcolando la derivata f’(x) della funzione f(x) e sostituendo al posto della x il valore dell’ascissa del punto di tangenza, nel nostro caso +2. Il valore che si ottiene è il coefficiente angolare m della retta.
calcoliamo la derivata della funzione 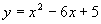
y’ = 2x – 6
sostituendo al posto di x +2 si ha m = 4-6 = -2
lo stesso valore di m che avevamo trovato prima.
----------------------------------------------------------------------------------------------------------------------
Risolviamo la seguente disequazione frazionaria:
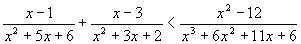
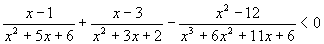
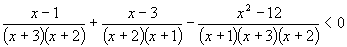
facendo gli opportuni calcoli si giunge alla seguente disequazione:
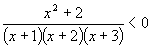
a questo punto poniamo il numeratore maggiore di 0 ed anche ogni fattore del denominatore maggiore di 0
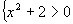
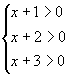
la prima disequazione(numeratore) è verificata per qualsiasi valore di x (positivo o negativo)
la seconda per x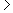 -1 -1
la terza per x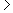 -2 -2
la quarta per x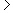 -3 -3
rappresentiamo ora su una retta ognuno dei quattro fattori in modo che i valori di x che rendono positivo il fattore siano rappresentati da una linea continua mentre i valori di x che rendono negativo il fattore siano rappresentati da una linea tratteggiata.
Consideriamo che la disequazione è frazionaria e che tale quoziente è minore di zero se uno dei due termini
è minore di zero.
Consideriamo ancora che il denominatore è il prodotto di tre fattori.
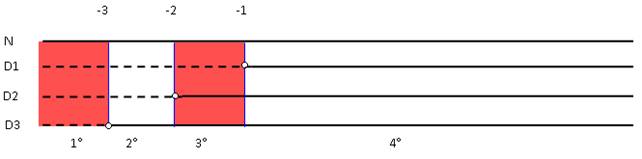
Denominatore = D1*D2*D3
Nel primo intervallo il numeratore è positivo, il denominatore è complessivamente negativo, la frazione sarà quindi negativa e quindi la disequazione è verificata.
Nel secondo intervallo il numeratore è positivo, il denominatore è complessivamente positivo, la frazione è positiva e quindi la disequazione non è verificata.
Nel terzo intervallo il numeratore è positivo, il denominatore è complessivamente negativo, la frazione è negativa e quindi la disequazione è verificata.
Nel quarto intervallo tutti i fattori sono positivi, la frazione è positiva e quindi la disequazione non è verificata.
Conclusione:
La disequazione è verificata per x < - 3 e per -2 < x < -1
----------------------------------------------------------------------------------------------------------------------
Vogliamo risolvere il seguente problema:
Costruire il grafico della funzione y = x3 –3x. Si determinino i punti d’intersezione del grafico con la retta y = x e si calcoli la misura dell’area della porzione di piano limitata dalla retta e dalla curva.
Il grafico è il seguente:
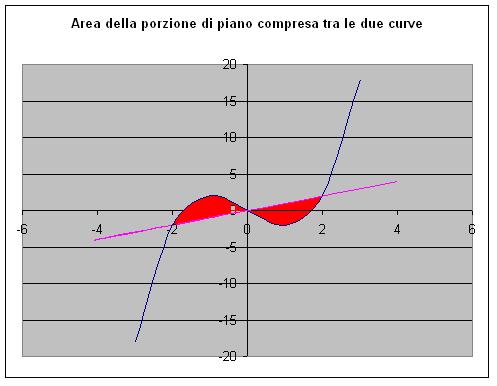
Con un semplice calcolo si determinano le ascisse dei punti di intersezione delle due curve:
-2;0;+2
Le due funzioni sono dispari in quanto f(-x)=-f(x)
Poniamo:
f(x) = x
g(x = x3 –3x
Poiché nell’intervallo (0,2) f(x) è >= g(x)
possiamo scrivere:
A(0,+2) = 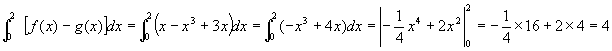
Area nell’intervallo (+2,-2) = 4*2 = 8 (8 rettangoli 1-1 espressi dalla figura)
-----------------------------------------------------------------------------------------------------------------
Studio della funzione y = 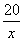
La funzione è definita e continua per tutti i valori di x ad eccezione di x = 0 . Si ha: D = R-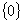
Poiché non è soddisfatta dalla coppia (0,0) non passerà per l’origine degli assi.
Verifichiamo la posizione che occupa nel piano cartesiano:
poniamo 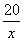 >0 >0
la funzione è positiva se x è positivo, è negativa se x è negativo, quindi dovrà occupare il primo e il terzo quadrante.
Verifichiamo se è simmetrica rispetto all’origine degli assi:
f(-x) = -f(x)
f(-1) = - 20
f(+1) = 20
è verificata la condizione.
È una funzione dispari.
Verifichiamo se l’asse delle y è un asintoto verticale:
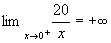 e e 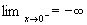
l’asse delle y è un asintoto verticale
verifichiamo se lo è anche l’asse delle x
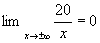
l’asse delle x è un asintoto orizzontale
Calcoliamo ora la derivata prima:
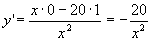
poniamo la funzione maggiore di 0
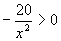
per qualsiasi valore di x (escluso x = 0) la funzione è negativa.
Ne consegue: da -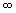 a 0 la curva è decrescente (quando i valori di y aumentano in senso negativo diventano via via più piccoli); da 0 a + a 0 la curva è decrescente (quando i valori di y aumentano in senso negativo diventano via via più piccoli); da 0 a + 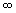 la curva è ancora decrescente la curva è ancora decrescente
Non esistono valori di x che uguagliano a 0 la derivata prima: non ci sono punti di flesso.
Calcoliamo la derivata seconda:
y’’ = 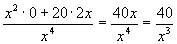
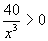 per x>0 quindi nel primo quadrante la concavità è verso l’alto per x>0 quindi nel primo quadrante la concavità è verso l’alto
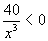 per x<0 quindi nel terzo quadrante la concavità è verso il basso per x<0 quindi nel terzo quadrante la concavità è verso il basso
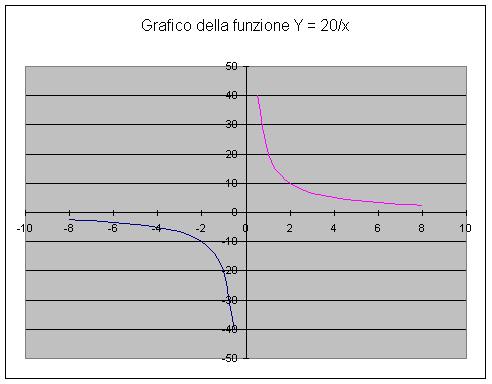
la curva, come sapevamo già dall’inizio, è una iperbole equilatera che occupa il primo e il terzo quadrante:
|

